Как научиться быстро считать в уме ребенку и взрослому

Умение быстро считать – это необходимый навык любого культурного человека. Базовые арифметические знания пригодятся при расчетах в магазине. Кроме того, развиваются внимание, память, концентрация, а мышление станет более собранным. Математика – сродни магии, здесь все четко и точно. Существует масса методик, как научиться быстро считать в уме, несколько из них разберем подробнее.

С чего начинать тренировку

Математика базируется на 4 простых действиях – сложении, вычитании, умножении и делении. Разобравшись в них один раз, достаточно заниматься по 5-10 минут в день, чтобы намного улучшить уровень счета. Составляющие успешного обучения:

• умение концентрировать внимание на поставленной задаче;
• знание основных формул;
• практика.

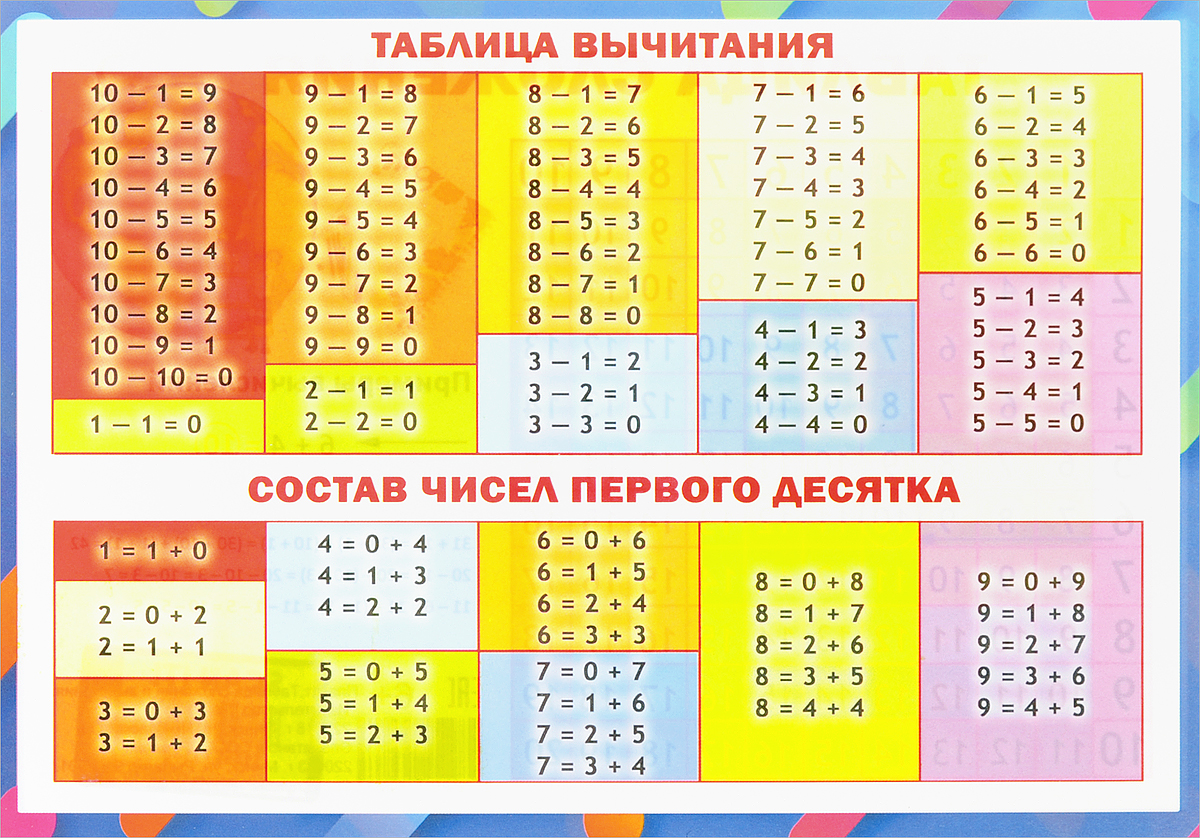
Начинают с самого простого – сложения однозначных чисел. Как только поиск правильного ответа займет не более 2 секунд, решают примеры с переходом через 10.

Технику называют «опора на десяток», например, складывают 7 и 8:

• сколько не хватает с 7 до 10 – тройки;
• представляют 8 как сумму 3 и второго «куска» – это 5;
• прибавляют к 7 тройку, как недостающее до 10, затем вторую часть (5);
• в итоге получают 15.

Простейшая техника ускорит счет.

Действие сложения

Рассмотрим, как взрослому научиться быстро считать в уме сложение многозначных чисел. Надо уметь складывать одинаковые разряды. Исходные данные разбивают на определенные разряды и складывают – тысячи с тысячами, сотни с сотнями и т.д. Разбивка «по старшинству» ускоряет сложение.

Пример сложения 456 и 789:

• разбивают 456 на 400, 50, 6;
• разбивают 789 на 700, 80, 9;
• складывают по разрядам, получая 1100, 130, 15;
• снова разбивают на части – 1100+100+30+10+5;
• в итоге получают 1245.

Таким же образом считают все многозначные числа.

Сложение и вычитание натуральных чисел базируется на правилах:

1. Если слагаемое увеличивают на какой-то показатель, его вычитают из полученной суммы. Например, (650+346+4) – 4. Решают так: (650+350) – 4 = 1000-4 = 996 или 650+346 = 996, обе 4 здесь «снимают», поскольку +/- одинакового числа дает в сумме 0.
2. Если к одному слагаемому добавляют показатель, из второго вынимают это же число – сумма не меняется. Например, (350+5)+(240-5) = 340+240 = 580, здесь +/- 5 = 0.

Таким образом всегда решают примеры с простыми числами. Техника поможет, если стоит вопрос, как быстро научиться считать сдачу. Ее легко освоит ребенок, знакомый с первыми простейшими действиями – сложение/вычитание.

Действие вычитания

Начинают также с простейших однозначных и двузначных чисел первого, второго десятка. Помогает та же техника с «переходом через 10». Например, следует вычесть из 12 всего 8, действуют так:

• разбивают 12 на 10 и 2;
• из 10 вычитают 8 – равно 2;
• к 2 прибавляют остаток из 12 – тоже 2;
• в итоге получают 4.

Вычитание многозначных чисел немногим сложнее.

К примеру, надо решить 528-326:

1. Разбивают 528 на 500, 20, 8. Исходное 326 разбивают на 300, 20, 6.
2. Вычитают 500-300=200, 20-20=0, 8-6=2.
3. Складывают результат 200+0+2 = 202.

Пример решен.

Совет! Чтобы решить пример с вычитанием из 1000, каждую цифру вычитают из 9, последнюю из 10, результат складывают. Например: 1000-202 = (9-2)+(9-0)+(10-2) = 798.

Действие умножения

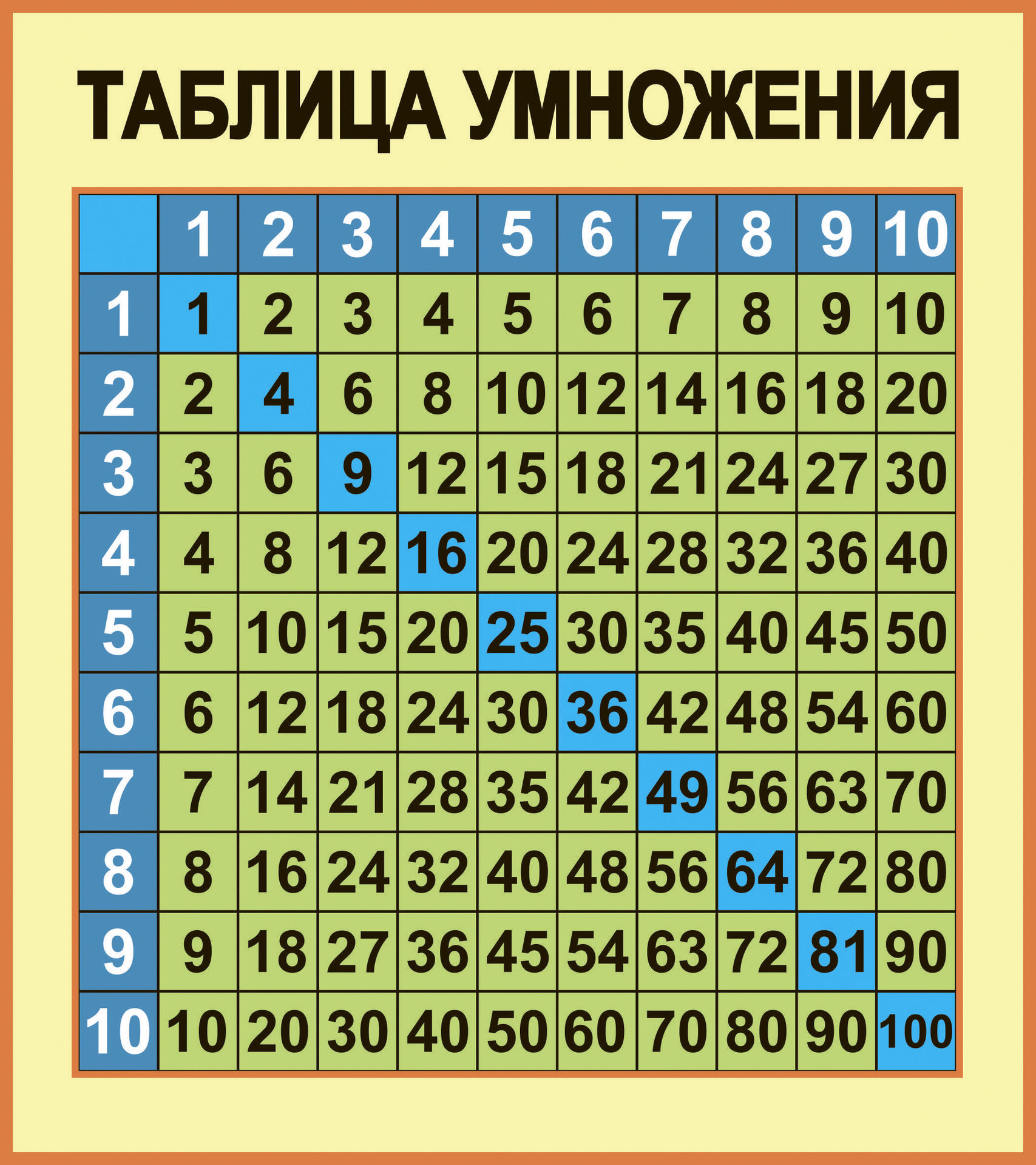
Если понимать, что умножение – это сложение одинаковых чисел определенное количество раз, ничего сложного в действии нет. Например, 4*7 = 4+4+4+4+4+4+4. В итоге получают 28. Упростит действие таблица умножения. Ее знает каждый школьник.

На заметку! Самое сложное в таблице действие – умножение 7*8. Тут действует мнемотехническая техника «пять шесть, семь, восемь». В результате умножения 7 и 8 получают 56.

Чтобы правильно умножать числа, их сводят к простым. Рассмотрим техники умножения.

Умножение 9 и 11

Правило при умножении на 9 умножают на 10 и вычитают 9. Если умножают на 11, сначала умножают на 10, прибавляя исходный показатель.

Пример:

• 15*9 = 15*10-15 = 150-15 = 135;
• 57*11 = 57*10+57 = 570+57 = 627.

Интересно! Чтобы возвести в квадрат число, оканчивающееся на 5, умножают десяток на десяток +1 и дописывают 25. Например: 35*35 = 3*(3+1) и дописывают 25 = 1225.

Умножение на 5 чисел до 10

Эта техника поможет правильно умножать двух-, трехзначные числа. Правило простое – множитель делят на 2. Получив результат в виде целого показателя, добавляют в конце 0, а если число не целое, отбрасывают остаток и добавляют в конце 5.

Пример 1482*5 решают так:

• (1482/2) _ (+0 или +5) = 741 _ (+0) = 7410 – исходный показатель делили на 2 без остатка;
• 2269-5 = (2269/2) _ (+0 или +5) = 1134,5 _ (+5) = 11345 – исходный показатель делили на 2 с остатком.

Техника, как быстро научиться считать деньги, умножая число на 5, 25, 50, 125 с использованием формул:

• А*5 = А*10/2;
• А*50 = А*100/2;
• А*25 = А*100/4;
• А*125 = А*1000/8.

Приставляя вместо А цифру, в процессе решения формулы получают нужный результат. Например, 25*25 = 25*100/4 = 2500/4 = 625.

Техника умножения на 4

Метод самый простой – исходный показатель умножают на 2, затем итог снова 2. К примеру, 2*4 = 2*2*2.

Умножение больших чисел с одним четным

В этом случае пользуются методикой упрощения множителей. Четное число уменьшают в 2 раза, а нечетное увеличивают в 2 раза. Например, 48*125 = 24*250 = 12*500 = 6*1000 = 6000.

Умножение многозначного числа на однозначное

Разбираясь, как научиться быстро считать деньги на кассе, пользуются техникой раскладывания на порядки, как в случае сложения. Пример 468*6 решают так:

1. Раскладывают 468 на 400, 60, 8. Умножают каждое число на 6.
2. Получают (400*6) = 2400 + (60*6) = 360 + (8*6) = 48. Итого 2400+360+48 = 2808.

Более сложный вариант с перегруппировкой итоговых результатов выглядит так: 2400+360+48 = 2000+400+300+60+48 = 2000+700+108 = 2808.

Умножение простых чисел

Диагональный метод нужен при поисках техники как быстро научиться считать устно. Заключается способ в дописывании числа, которого «не хватает до 10».

Пример 7*8 решают так:

• высчитают недостающее до 10 – в 7 это 3, в 8 это 2;
• затем 8-3 = 5;
• 3*2 = 6;
• в итоге получают 56.

Умножение чисел от 10 до 20

Правило – к одному числу прибавляют единицы другого, а сумму умножают 10. К результату добавляют сумму единиц. Например, 13*15 = (13+5)*10 + 3*5 = 180+15 = 195.

Умножение двузначных чисел

Упрощают процесс снова разложением двузначных чисел на простые действия. Пример 78*56 решают так:

1. В итоге должно получиться сложение цифры 78 точно 56 раз. Сначала складывают 78 пятьдесят раз, затем еще 6 раз.
2. Считают 78*5 = 70*5 + 8*5 = 350+40 = 390*10 = 3900.
3. 78*6 = 70*6 + 8*6 = 420+48 = 468.
4. 3900+468 = 3000+900+400+60+8 = (3000+1300+60+8) = 4368.

Пользуясь принципом упрощения и раскладывания больших чисел на разряды, умножают все двузначные числа.

Умножение на 9, 99, 999

Учитывают правило прибавления недостающих единиц. Пример 154*99 решают так: 154*(100-1) = 15400-154 = 15246. Таким же образом умножают на 9, 999.

Возведение в квадрат

Это тоже умножение, при котором число раскладывают на составляющие. Сначала находят произведение первой цифры на следующую за ней, результат будет заканчиваться на квадрат последней цифры. Пример возведения 75 в квадрат решают так: 7*8 = 56; 5*5 = 25. В итоге 75*75 = 5625.

Техника деления

Математическая формула деления – это «обратное» умножению. То есть при умножении складывали, а при делении вычитают. Чтобы разделить 56 на 7, подбирают число, при умножении которого на 7 в итоге будет 56. Зная таблицу умножения, сделать это просто, искомое число 8.

При делении многозначного числа на однозначное от исходного показателя «отрезают» круглые части, каждая из которых будет делиться на 8, в соответствии с таблицей умножения.

Пример 6144/8 решают так:

1. Из 6144 выделяют максимально большую часть, делимую на 8. Это 5600, поскольку следующее число по таблице умножения 64.
2. 6144-5600 = 544.
3. Итого 6144/8 = (5600+544)/8 = 700+544/8.
4. Чтобы поделить 544 на 8, снова выделяют из числа большую часть, делимую на 8 по таблице умножения. Это будет 480. В итоге получают остаток 64, поскольку 544-480 = 64.
5. Продолжают деление 544/8 = (480+64)/8 = 60+64/8.
6. Вспоминают все полученные ранее результаты: 700+60=760, решают задачу 64/8 = 8.

В итоге получают 760+8 = 768.

Техника деления на двузначное число

Эта самая гениальная техника, ни на что не похожая. Решая пример 5148/66, делают так:

• подгадывают, в каком десятке будет лежать результат;
• получают 70, поскольку при решении 70*66 = 4620, это самое близкое число к исходному делимому 5148;
• применяют математический закон о последней цифре результата умножения двух чисел – она всегда совпадает с последней цифрой результата умножения;
• получают искомое число, которое при умножении на 66 дает 5148 – это будет окончание на 3 или на 8 (3*6 = 18, 8*6 = 48);
• считают по окончаниям в десятке между 70 и 80 – находят всего два числа 73 и 78;
• теперь умножают 78*66 = 78*60+78*6 = 4680+468 = 500+148 = 5148.

Правильный ответ примера 5148/66 = 78.

Деление на 5, 50, 25

Применяют правило – умножают число на 2 и перемещают запятую на одну цифру назад. Например, 145/5 = 145*2 = 290, смещение запятой назад дает в итоге 29.

При делении на 50, 25 применяют формулы:

• А/50 = А*2/100;
• А/25 = А*4/100.

Например, 2350/50 = 2350*20/100 = 4700/100 = 47 и т.д.

Самые простые техники быстрого счета

Если что-то показалось сложным, есть ряд методик быстрого счета:

1. Как быстро научиться считать проценты. Чтобы найти 15% от числа, находят 10% и добавляют половину от 10%. Например, 15% от 664 = (10%) + (10%/2) = 66,4+33,2 = 99,6. Таким же образом раскладывают другие числа на составляющие.
2. Умножая двузначное число на однозначное, раскладывают первое на две части. Например, 45 раскладывают на 40 и 5. Затем производят технику умножения каждой части и сложение итоговых результатов.
3. При умножении трехзначных чисел также раскладывают его на части. Например, 137*5 решают так: 100*5 + 30*5 + 7*5 = 500+150+35 = 650+35 = 685.
4. Умножение на 10 решают приписыванием к основному числу нуля. Например, 100*10 = 1000.
5. Умножение на 5 решают так: число умножают на 10, затем делят на 2. Например, 568*5 = (568*10)/2 = 5680/2 = 5000/2+600/2+8/2+0/2 = 2500+300+4+0 = 2840.
6. Умножение на 11 выполняют так – мысленно раздвигают начальное число и вписывают сумму крайних чисел. Например, 18*11 = 1_(1+8=9)_8 = 198.
7. Умножение на 1,5 выполняют так – число делят на 2 и прибавляют полученную половину к целому. Например, 24*1,5 = 24/2+24 = 36.
8. Умножение на 5 делают * на 10 и делением на 2.
9. Умножение на 6 делают так (х*3)*2.
10. Чтобы умножить на 12, сначала умножают на 10 и дважды добавляют исходное число. Например, 12*12 = 12*10+12+12 = 120+12+12 = 120+24 = 144.
11. Умножая на 13, сначала умножают на 3 и 10 раз добавляют исходное число. Например, 3*13 = 3*3+10*3 = 9+30 = 39.
12. Умножая на 14, умножают на 7, затем на 2.
13. Умножая на 15, выполняют умножения на 10, затем 5 раз добавляют исходное число.
14. Умножая на 16, умножают на 8, затем на 2.
15. Умножение на 17 выполняют умножением на 7, затем 10 раз добавляют исходное число.
16. Чтобы умножить на 18, делают умножение на 20 и два раза отнимают исходное число.
17. Умножая на 19, умножают на 20 и один раз отнимают исходное число.

Совет! Чтобы умножить на нецелое число (19, 27, 39 и т.д.), сначала умножают на большее целое, затем отнимают исходное число нужное количество раз. Например, 3*39 = 3*40-3 = 120-3 = 117.

Как считать чаевые в процентах

Быстрое определение суммы чаевых – обязательная мера в кафе или ресторане. Иногда в заведениях общепита уже заложены чаевые и тут важно быстро считать, чтобы пользователя не обманули.

Например, вычисление 7% от 300 делают так:

• раскладывают большое число на сотни;
• из каждой 100 считают 7%, это 7;
• складывают количество высчитанных процентов по количеству сотен = 7+7+7 = 21.

Итого 7% от 300 = 21. Точно таким же образом считают все проценты. Поняв, что 1% из 100 равен 1, легко вычислить необходимую сумму выплат. Например, 5% от суммы чека в 1650 рублей составят: (5% от 1000 = 50) + (5% от 600 = 30) + (5% из 50 = 2,5) = 50+30+2,5 = 82,5 рубля. Итого сверх суммы обеда чаевые полагаются не более 82,5 руб.

Вот и все премудрости. Зная их, взрослый никогда не ошибется в сдаче на кассе, рынке. Также будет просто объяснить правила математики малышу.

Как ребенку научиться быстро считать в уме:

• тренироваться каждый день вместе с родителями;
• считать собственные деньги, затраты.

Тут многое делают родители, отправляя ребенка в магазин и поручая считать сдачу. Быстрее всего учатся считать на деньгах. И именно эти знания затем пригодятся в жизни.